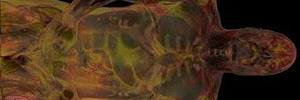
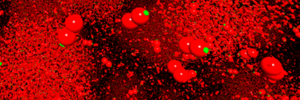
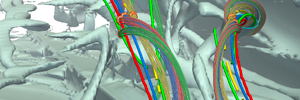
Volumenvisualisierung
Erzeugung interaktiver Bilder aus skalaren 3D-Daten, etwa zur medizinischen Bildgebung oder zur Visualisierung komplexer Simulationen aus der Strömungsmechanik, Geologie oder Seismologie.
Molekulardynamik-Visualisierung
Partikelbasierte Computersimulationen sind nicht leicht zu analysieren, insbesonders bei unerwarteten Effekten. Interaktive Visualisierungen sollen diesen Prozess effizienter gestalten.
Strömungs-, Vektorfeld-, Tensorfeldvisualisierung
Vektoren oder Tensoren werden verwendet, wenn Richtungsinformationen eine Rolle spielen, etwa beim Strömungsverhalten von Luft oder bei der Darstellung von Nervenbahnen im Gehirn.
Proteindynamik und Systembiologie
Ein Schlüssel zu neuen Erkenntnissen in der Protein- und Systembiologieforschung sind Simulationen. Neue Visualisierungstechniken können das Erfassen der komplexen Daten ermöglichen.
Astronomische Daten und Objekte
Reale astronomische Objekte naturgetreu am Rechner rekonstruieren – dazu entwickeln wir geeignete und schnelle Visualisierungsmethoden. So entstehen aus 2D-Bildern interaktive 3D-Objekte.
Texturbasierte Strömungsvisualisierung
Vektorfelder werden häufig durch Glyphen dargestellt. Texturbasiert bedeutet im Gegensatz dazu, dass jedem Bildpunkt eine Richtungsinformation zugeordnet wird, um eine möglichst dichte Repräsentation zu erhalten.
Relativistische Visualisierung
Die aus der Relativitätstheorie resultierenden Effekte entziehen sich unserer Alltagserfahrung. Computersimulationen eröffnen uns einen intuitiven Zugang zu Phänomenen dieses Bereiches.